jueves, 15 de diciembre de 2011

Definición de función definida por secciones.

     
Las funciones por partes son funciones que están divididas en dos o más expresiones, cada uno de los cuales obedece a un comportamiento diferente.
Las funciones indican el intervalo en que se encuentra definido en cada sección. Estos intervalos son los valores que toma la variable independiente x, por eso se consideran sobre el eje x. Los intervalos pueden ser expresados mediante desigualdades.
En términos matemáticos, una función por secciones es aquella función en que el dominio se divide en subconjuntos, y para cada uno de estos subconjuntos se define una función distinta, al definir una función por secciones los intervalos de definición tienen que estar bien establecidos, esto es, una condición para que f sea una función es que a cada valor de x le corresponda uno y sólo un valor de y. Si a x le corresponde más de un valor de y, o si no le corresponde ninguno, no se establece la función.

miércoles, 7 de diciembre de 2011

martes, 18 de octubre de 2011

Historia del Cálculo

     
Después de la Construcción del Cálculo la historia de la matemática ya no fue igual: la geometría, el álgebra y la aritmética, la trigonometría, se colocaron en una nueva perspectiva teórica. Detrás de cualquier invento, descubrimiento o nueva teoría, existe, indudablemente, la evolución de ideas que hacen posible su nacimiento. 

domingo, 21 de agosto de 2011

Sustancias que funcionan como súper proteínas

     

Un grupo de ingenieros en biotecnología realizaron una investigación para crear una sustancia que funcionara como una súper proteína en un tipo especial de microorganismos que habita cerca de una zona petrolera. El objetivo es hacer dichos microorganismos más resistentes y, en el caso de que existiera algún derrame petrolero cerca de la zona, utilizarlos para la limpieza de algún derrame.
Durante la investigación, se presentaron muchas dificultades, se tenían previstos tres proyectos diferentes, los cuales resultaron en un rotundo fracaso. En cada uno de los proyectos se desarrolló una sustancia diferente, al realizar las pruebas con tales sustancias, éstas no mejoraron los microorganismos como se esperaba, de esta manera, los frascos que contenían las sustancias respectivas de cada proyecto fueron vaciados a un mismo contenedor con capacidad de m litros, el cual se encontraba completamente limpio. Los ingenieros tomaron una muestra de la sustancia que resultó de la combinación de las tres que se vaciaron al contenedor y observaron los resultados, luego de ponerla en el microscopio. Esta muestra era producto de un accidente científico.
Después de esto, cada grupo hizo una marca al recipiente que contenía su respectiva sustancia, esto, con el objeto de tener en cuenta la medida que utilizaron y relacionarlo con el resultado que se obtuvo. De esta manera, volvieron a utilizar la misma medida que vaciaron al contenedor para formar una nueva sustancia, la probaron y el resultado fue exactamente el mismo que el que había en el contenedor.
Después de esto, todos se dieron cuenta de que nadie sabía exactamente cuánto fue lo que depositó de su respectiva sustancia, pero tenían el recipiente en el que señalaron la medida. Para saber las cantidades exactas, sugirieron formar un sistema de tres ecuaciones para encontrar los valores exactos de los recipientes de cada uno de los grupos, de esta manera, realizaron las siguientes pruebas.
1.      Utilizaron 2 vasos de la primera sustancia, 2 vasos de la segunda y un vaso más de la tercera, obteniendo 4.5 litros de la sustancia final.
2.      Utilizaron 4 vasos de la primera sustancia, 6 vasos de la segunda y 3 vasos más de la tercera, obteniendo 12 litros.
Nota: Para encontrar lo que se te pide, supón que en las primeras dos pruebas (la del accidente y la repetición del mismo) se colocaron 6 vasos de la primer sustancia, 9 vasos de la segunda y 7 vasos de la tercera.
Ordenando los datos del problema

Sea:
S1 la cantidad total de la sustancia del proyecto 1.
S2 la cantidad total de la sustancia del proyecto 2.
S3 la cantidad total de la sustancia del proyecto 3.
MP la cantidad en litros de cada proyecto

La cantidad total al vaciar todas las sustancias estará dada por la siguiente ecuación

M (litros) = S1 + S2 + S3 ------------------------ (ECUACIÓN A)


Los datos del problema se pueden organizar en una tabla (matriz) de la siguiente manera

Pruebai/sustancias
S1 (vasos)
S2(vasos)
S3(vasos)
MP (lts.)
P1
2
2
1
4.5
P2
4
6
3
12.0
P3
6
9
7
X
Total de sustancia
12
17
11
16.5+X

De la tabla anterior podemos representar cada uno de los proyectos mediante ecuaciones lineales de primer grado toda vez que cumplen la características de este tipo de ecuación ya que los coeficientes están elevados a X1
Ya que los datos de los distintos proyectos están relacionados entre si, podemos decir que tenemos un sistema de tres ecuaciones lineales con 4 incógnitas, expresando por el siguiente sistema:

P1 = (2)S1+ (2)S2+(1)S3 = 4.5 lts--------------Ecuación 1
P2 = (4)S1+(6)S2+(3)S3 = 12 lts--------------Ecuación 2
P3 = (6)S1+(9)S2+(7)S3 = X lts--------------Ecuación 3

El contenido del recipiente donde se vaciaron todos los experimentos estará dado por la siguiente expresión:

PT = (12)S1T+(17)S2T +(11)S3T = 16.5+ X lts--------------Ecuación 4
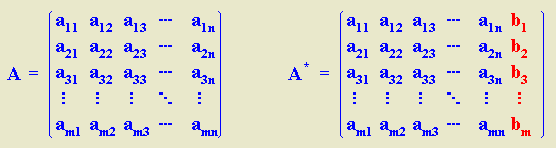
Aunque el sistema de ecuaciones antes descrito se puede expresar mediante un arreglo de matricial de la forma:

a11x1+ a12x2+ … a1n xn = b1
a21x1+ a22x2+ … a2n xn = b2
…        …..          ……      …
Am1x1+ am2x2+ … amn xn = bm
Donde:
Donde x1, x2, ... xn son las incógnitas y los números aij Î K

En el caso de el sistema de ecuaciones 1,2,3 pudría representarse como matriz de coeficientes por ser  un sistema de ecuaciones lineales, pero para solucionar el problema requerimos de una matriz ampliada que represente a la matriz de los coeficientes de lado izquierdo de la igualdad de las ecuaciones 1,2 y 3 y otra que representa a la matriz de constantes de las mismas ecuaciones pero en este caso no se cumple ya que en la ecuación 3 tenemos una incógnita, representada por X lts.

Luego entonces la solución de nuestro sistema seria:...... lo demas lo puedes hace tu sin problemas

Esad El desarrollo de Noruega

     

Introducción
En este informe se presenta la investigación sobre Desarrollo Humano del Reino de Noruega, considerando que este país es hasta el día de hoy el país que ocupa el número uno en Desarrollo Humano del mundo, para esta investigación se consideró como fuente principal el Programa de Naciones Unidas para el Desarrollo.
Los resultados que se presentan en esta investigación van de lo general a lo particular en primer lugar se muestran los incides generales que Noruega a obtenido de 1980 a 2010, posteriormente se muestran los resultados medidos de los Índices de Desarrollo Humano de manera global para posteriormente presentar la información particular o desglosada por cada grupo de indicadores.
 
Consideraciones Generales
El desarrollo de un país se refiere a la forma a la distribución armoniosa, integral y del crecimiento económico y los logros sociales, a la independencia social y monetaria en referencia a ese crecimiento de la población, lo que reditúa en cambios en sus actitudes sociales, en las técnicas de producción y comercio y sirven de base para un desarrollo íntegro.
El desarrollo Humano no es solo el aumento o disminución del ingreso nacional, este tiene que ver con que las personas vivan en un entorno para que se hagan realidad sus posibilidades de vida y sea esta productiva y creadora de acuerdo con sus necesidades e intereses, no solo su crecimiento económico que es solo un medio que ampliar sus opciones.
El desarrollo humano tiene que ver con que la población de un país tenga una vida larga y sana, tener conocimientos, tener acceso a los recursos necesarios para alcanzar un nivel de vida decoroso y poder participar en la vida de la comunidad, también tiene que ver con los derechos humanos; su objetivo es la libertad humana, vital para el desarrollo de las capacidades y el ejercicio de los derechos.
La población de un país deben tener libertad para hacer uso de sus opciones y participar en las decisiones políticas y sociales que afectan sus vidas y garantizar el bienestar y la dignidad de todas las personas y fomentan el respeto por sí mismo y por los demás.
Para que se produzca un desarrollo hace falta que los Índice de Desarrollo Humano (IDH) sean los mejores, un indicador De Desarrollo Humano es el propuesto por el Programa de Naciones Unidas para el Desarrollo PNUD.
El Índice de Desarrollo Humano (IDH) fue creado en 1990 a través del Programa de las Naciones Unidas para el Desarrollo (PNUD). El objetivo era poder medir los progresos generales de un país en tres dimensiones básicas del desarrollo humano. Para cada dimensión habían elegido una variable que la representaba
Según estos indicadores los países se clasifican según su IDH en tres grupos:
·                                 Países con desarrollo humano alto: con valores del IDH de 0,800 y superiores;
·                                 Países con desarrollo humano medio: con valores entre 0,500 y 0,799;
·                                 Países con desarrollo humano bajo: con valores inferiores a 0,500.
De acuerdo con los Resultados de PNUD de 2010, de los 162 países de los cuales se calculó el IDH, 48 están en la categoría de alto desarrollo humanó, 78 en la categoría mediana y 36 en la categoría baja, siendo Noruega con (0,938) el numero uno en Desarrollo Humano

miércoles, 29 de junio de 2011

eliminar virus Recycler

     
Un troyano molesto poco dañino perro que crece y gracias a que se trasporta por en Archivos de configuración de inicio de Windows  Autorun.inf, que se infiltra en memorias USB.
Cuando una computadora se encuentra infectada por el virus recycler, este se aloja en la carpeta "Recycler" dentro del disco duro, mismo lugar en donde se almacena toda la "basura" (archivos y carpetas que eliminamos) de la la carpeta de reciclaje cuando ésta no se ha vaciado o restaurado. El virus toma posesión de la carpeta y se esconde dentro de otra subcarpeta simulando ser una aprte de los archivos de la papelera de Recyclaje, pero desde ésta ubicación reproduce múltiples copias de si mismo y llena de basura el registro de Windows. Lamentablemente, al alojarse en un directorio de sistema, muy pocos son los antivirus que han podido eliminarlo sin que el virus deje rastro.
A pesar de que se puede acceder hasta la ubicación del archivo para eliminarlo, al tener por defecto los permisos restringidos, este se vuelve casi imposible de elimanar por el usuario, a no ser que se intente elimnarlo desde la línea de comandos de Windows. Y precisamente, este es uno de los trucos para eliminarlo, usando el Símbolo del Sistema de Windows XP:
  1. Abrir una ventana de comandos (Se puede hacer con  el comando "cmd" en Inicio -> Ejecutar). A continuación, los comandos que aparecen en cursiva deben teclearse dentro de la linea de comandos de cmd.
  2. Finalizar el proceso del explorador (explorer.exe):

    taskkill /f /im explorer.exe
  3. Movernos a la carpeta del virus, con:

    cd \Recycler
  4. Quitar los atributos de la carpeta \S-1-5-21-1482476501-1644491937-682003330-1013\ con el comando:

    attrib -h -r -s S-1-5-21-1482476501-1644491937-682003330-1013
  5. Ahora debemos renombrar la carpeta, con cualquier nombre (en el ejemplo usamos "virus":

    ren S-1-5-21-1482476501-1644491937-682003330-1013 virus
  6. Reiniciar el explorador de windows con el comando:

    explorer.exe.
  7. Ya en el explorador de Windows, debemos ir a la carpeta Recycler y veremos nuestra carpeta llamadavirus. Accedemos a la carpeta y simplemente eliminamos todo su contenido: ise.exe, isee.exe y desktop.ini.
  8. Opcionalmente podemos también limpiar la ruta del registro HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Active Setup\Installed Components\{08B0E5C0-4FCB-11CF-AAX5-90401C608512}. Para ello, accedemos al registro de Windows con el comando "regedit" desde Incio -> Ejecutar.
Estos pasos tambiñen funcionan para limpiar memorias flashUSB, cambiando la unidad C: por la que corresponda a la unidad extraíble y omitiendo el paso de la limpieza del registro. Una vez concluída la limpieza, es recomendable el uso de algún software limpiador del sistema como CCleaner.

martes, 14 de junio de 2011

Ejercicios de factor de conversión

       No comments

1.      Obtén la masa de 10 litros de mercurio (densidad del mercurio: 13,6 kilogramos por decímetro cúbico).
13.6 g/cm3*1Kg/1000g=0.0136 Kg/cm3
0.0136 Kg/cm3*1'000.000cm3/m3=13600 Kg/m3

entonces la densidad del mercurio en Kg/m3 sera 13600

lo importante en este ejercicio es recordar que en un m3 hay 1000000 cm3


listo:)
 
Entonces lo que primero debemos hacer es convertir de litros a m³ porque al densidad esta en kg /m³. 1 m³ son 1000 litros, entonces:

10[L] /1000[L /m³] = 0.010[m³]

La formul de densidad (ρ) es la siguiente

ρ = m /V

donde
m = masa
V = volumen

Sustituyendo lso datos en la ecuaicon podemos obtener al amsa despejandola

13600[kg/m³] = m /0.010[m³]

13600[kg/m³] ·0.010[m³] = m

136[kg] = m

El peso en magnitud (P), tiene la siguiente formula

P = m ·g

donde
g = magnitud de la aceleracion de gravedad (9,8[m/s²] en la tierra)

P = 136[kg] ·9,8[m/s²]

P = 1333[N]


2. Convierte 242º a radianes (factor de conversión: 180º = π rad).



3. Si una bola de acero pesa 14 lb, ¿cuál será su peso en kilogramos? Considera que una libra equivale a 0.454 kg.



4. Un automóvil recorrió 250 millas, si una milla equivale a 1609 metros, ¿cuál es la distancia en metros?



5. Una persona tiene una talla de 6 pies 6 pulgadas (6’6’’), si una pulgada equivale a 2.54 cm, ¿cuál es la talla en metros?


lunes, 13 de junio de 2011

Un poco de historia del álgebra lineal

     
agosto 3rd, 2010 Escrito por Jesus Soto

La Teoría de Matrices y el Algebra Lineal no aparece como consecuencia del estudio de los coeficientes de los sistemas de ecuaciones lineales. La organización de estos coeficientes llevó al desarrollo de los determinantes y no de las matrices (Leibniz utilizó determinantes en 1693 y Cramer desarrolló su método de resolución de sistemas mediante determinante en 1750). El primer uso implícito de las matrices aparece en la obra de Lagrange en su estudio de los extremos de funciones de varias variables a finales del siglo XVIII.
El hecho que llevó al desarrollo de las matrices fue el concepto de multiplicación, dado por Cayley en 1855, para representar la composición de aplicaciones (transformacion ) lineal . Fue Sylvester, en 1848, el que acuñó el término "matriz" pues consideraba una matriz como un generador de determinantes: cada subconjunto de k filas y k columnas de una matriz generaba
un determinante kxk. Con el resultado ”det(AB) = det(A)det(B)” se estableció una conexión entre las teorías de las matrices y los determinantes.
El siglo XX focalizó sus intereses en el estudio de espacios vectoriales abstractos, relegando las matrices al papel de una notación en la interpretación del comportamiento de las aplicaciones lineales. Hubo que esperar al final de la II Guerra Mundial, con el advenimiento de los computadores, para que se volviera a enfatizar el estudio de las matrices como entes con interés propio. Alan Turing introduciría en 1948 el concepto de LU-factorización y una década después aparecería el concepto de QR-descomposición (Wilkinson) y la constatación de la estabilidad del método de eliminación gaussiana, que sigue siendo el mejor método conocido para la resolución de los sistemas de ecuaciones lineales.
(Extraído del texto indicado)

martes, 7 de junio de 2011

Matrices: definición, operaciones y propiedades básicas.

     
    En este tema estudiaremos las matrices como objeto matemático y su aplicación al estudio de los sistemas de ecuaciones lineales. Veremos sus propiedades fundamentales, las operaciones básicas, y una aplicación importante de estos conceptos: el Teorema de Rouché-Frobenius.


3. TEOREMA DE ROUCHÉ-FRÖBENIUS
Antes de proceder a resolver un sistema de ecuaciones lineales, tenemos que dar respuesta a las siguientes preguntas: ¿El sistema tiene solución, es decir, es compatible? En caso afirmativo: ¿Tiene una solución o infinitas? Para responderlas, una de las herramientas que podemos utilizar es la que proporciona el Teorema de Rouché-Fröbenius, cuyo enunciado es el siguiente:
Consideremos un sistema de  m  ecuaciones lineales con  n  incógnitas, cuya expresión general es la siguiente:
Sean  A  la matriz del sistema  y  A*  la matriz ampliada del sistema (con los términos independientes).
La condición necesaria y suficiente para que un sistema de  m  ecuaciones lineales con  n  incógnitas sea compatible es que el rango de la matriz de los coeficientes de las incógnitas ( A )  sea igual al rango de la matriz ampliada con los términos independientes  ( A* ). Es decir:  rango (A) = rango (A*).
Si el valor común de los rangos coincide con el número de incógnitas, el sistema es compatible determinado. Si, por el contrario, el valor de los rangos es menor que el número de incógnitas el sistema es compatible indeterminado.
En resumen:
  • Si rango (A) = rango (A*) = n (número de incógnitas), el sistema es compatible determinado (tiene una única solución).
  • Si rango (A) = rango (A*) < n (número de incógnitas), el sistema es compatible indeterminado (tiene infinitas soluciones).
  • Si rango (A) # rango (A*), el sistema es incompatible (no tiene solución).
Un caso particular es el de los sistemas homogéneos, es decir, aquellos en los que todos los términos independientes son nulos. Pues, en este caso, las matrices  A  y  A*  son  semejantes a efectos del cálculo del rango, dado que la matriz  A*  es la matriz  A  a la que se le añade una columna de ceros, que podemos suprimir para calcular el rango. Por lo tanto, siempre se cumple que rango (A) = rango (A*). Esto quiere decir que todos los sistemas homogéneos son siempre compatibles. Se cumple:
  • Si rango (A) = n (número de incógnitas), el sistema es compatible determinado. Tiene una única solución, que se conoce con el nombre de solución trivial. Es aquella en la que todas las incógnitas son  nulas  ( 0 ).
  • Si rango (A) < n (número de incógnitas), el sistema es compatible indeterminado (tiene infinitas soluciones).
Una vez realizada la "discusión o identificación del sistema", aplicaremos alguno de los métodos que desarrollaremos en los epígrafes posteriores. No obstante, es preciso tener en cuenta las siguientes observaciones:
  • Si el sistema es compatible determinado, el valor común de los rangos indica el número de ecuaciones principales, es decir, aquellas que no dependen de las restantes.
  • Si el sistema es compatible indeterminado, (rango (A) = rango (A*) = k < n) el valor común de los rangos  ( k )  indica tanto el número de ecuaciones independientes o principales, como el número de incógnitas principales. Las restantes incógnitas  (no principales)  n - k  las pasaremos al segundo miembro formando un único término junto al término independiente. Siguiendo este procedimiento obtendremos un sistema de  k  ecuaciones lineales con  k incógnitas (principales), al que aplicaremos uno de los procedimientos que estudiaremos en los siguientes apartados: Regla de Cramer, Método de Gauss o, por la matriz inversa.

    http://recursostic.educacion.es/descartes/web/materiales_didacticos/sistemas_de_ecuaciones_lineales_2bcnt/discusion_por_el_teorema_de_rouche.htm